问题描述

一块边长是2L的正方形蛋糕落在坐标轴内，中心在原点上，现在你竖直切了m次，水平切了n次，中间还挖出了一个长度是2P的正方形的洞，洞的中心也在原点上。求最终蛋糕分成了几块。

输入格式

输入cake.in共四行。

第一行一个数L，第二行一个数P

第三行n个数，表示水平切的位置

第四行m个数，表示竖直切的位置

输出格式

一个数，表示最终那个蛋糕的个数

样例输入

5

3

1 -4

1

样例输出

6

数据范围

30% 的数据 L,P≤10,1≤n,m≤2

100%的数据 1≤L,P,1≤n,m≤100

题解

假设中间没有挖掉一个正方形的洞，那么，最终会有(n+1)*(m+1)个蛋糕。

而事实上中间挖掉一个正方形的洞，这对答案会有什么影响呢？

如图，

 

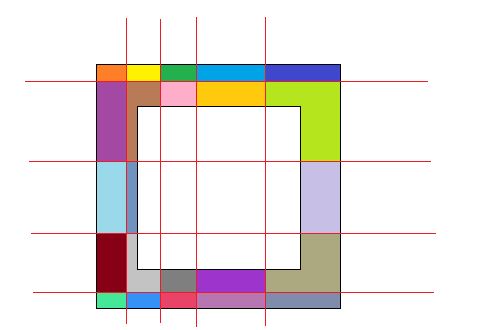
有几个小蛋糕完全被正方形的洞覆盖了，这些蛋糕不能算入答案的总个数。

假设水平切有px次经过挖掉的洞，竖直切有py次经过挖掉的洞，显然，完全被正方形覆盖的校蛋糕有(px-1)*(py-1)个；

最终答案就是(n+1)*(m+1)减去完全被洞覆盖的蛋糕数。

 

 

1 #include 
     
       2 #include 
      
        3 int L,P,ans,x[105],y[105],xt,yt,px,py; 4 bool visx[200],visy[200],vis; 5 int main() 6 { 7     int res,i,j,f; 8     char ch; 9     bool fg,mak;10     scanf("%d%d\n",&L,&P);11     for (ch=getchar();ch!='\n';ch=getchar())12     {13         res=0;  f=1;14         while ((ch<'0' || ch>'9') && ch!='-' && ch!='\n') ch=getchar();15         if (ch=='\n') break;16         if (ch=='-') f=-1,ch=getchar();17         while (ch>='0' && ch<='9')18           res=res*10+ch-'0',ch=getchar();19         res*=f;20         if (!visx[res+100]) visx[res+100]=1,x[++xt]=res;21         if (ch=='\n') break;22     }23     for (ch=getchar();ch!='\n';ch=getchar())24     {25         res=0;  f=1;26         while ((ch<'0' || ch>'9') && ch!='-' && ch!='\n') ch=getchar();27         if (ch=='\n') break;28         if (ch=='-') f=-1,ch=getchar();29         while (ch>='0' && ch<='9')30           res=res*10+ch-'0',ch=getchar();        31         res*=f;32         if (!visy[res+100]) visy[res+100]=1,y[++yt]=res;33         if (ch=='\n') break;34     } 35     for (i=1;i<=xt;i++) 36       if (-P<=x[i] && x[i]<=P)37         px++;38     for (i=1;i<=yt;i++)39       if (-P<=y[i] && y[i]<=P)40         py++;41     if (px<1) px=1;42     if (py<1) py=1;43     printf("%d",(xt+1)*(yt+1)-(px-1)*(py-1));44     return 0;45 }